CORSO DI CABRI GEOMETRE

di Luigi Pellegrini

10. Utilizzare cabri-géomètre nella geometria non euclidea

Costruire una macro per ognuno dei seguenti punti:

1.  Birapporto (A,B,C,D)=

2.  Hretta passante per P e Q

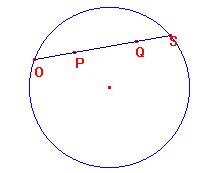
3.  Hdistanza tra P e Q=

4.  Htrasporto di lunghezza

Vogliamo trasportare il segmento AB secondo la metrica iperbolica su una hsemiretta di origine P e punto all’infinito S, cioè vogliamo costruire Q su PS tale che hdistanza(A,B) = hdistanza(P,Q)

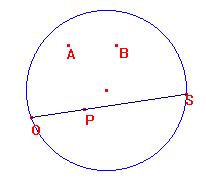
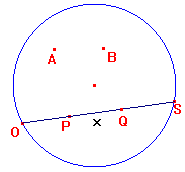
Sia x=distanza euclidea tra P e Q (punto da determinare)

sia d=hdistanza tra A e B.

Si ha:

Trasportando la distanza (euclidea!) x sulla semiretta PS otteniamo il punto Q.

5.  Hcompasso

Utilizzando la macro htrasporto di lunghezza htrasportare il segmento AB sulla hsemiretta di centro P e punto all’infinito S, ottenendo il punto Q:

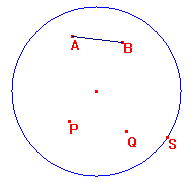
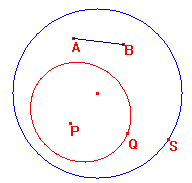
Il luogo generato da Q al variare di S sulla circonferenza iperbolica è lhcirconferenza di centro P e raggio AB. Provare a muovere tale circonferenza muovendo il punto P.

6.  Hasse di un segmento

Utilizzando la macro hcompasso si può costruire lhasse di un segmento, usando lo stesso procedimento che si segue nel piano euclideo.

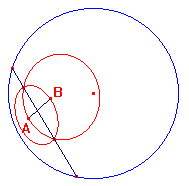
Si può analogamente costruire lhpunto medio di un segmento, lhperpendicolare ad un segmento in un estremo e passante per un punto esterno.