This is the page
27 Gennaio 2019
è arrivato … il Cantastoria
27 Gennaio 2019di Luigi Pellegrini
11. Cabri-géomètre e il problema di Apollonio
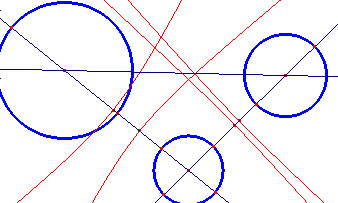
Problema di Apollonio: date 3 circonferenze, trovare tutte le circonferenze che sono tangenti contemporaneamente alle circonferenze date.
Partiamo da 2 circonferenze di centri O e O e raggi rispettivi R e r. Il centro P di una circonferenza tangente a entrambe descrive il ramo di uniperbole: infatti PO-PO= R-r = cost. I fuochi sono O e O mentre i punti di intersezione con la retta OO sono M (punto medio di ab) e N (punto medio di cd).
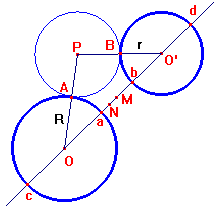
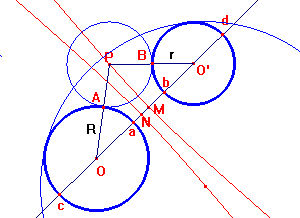
L’altro ramo dell’iperbole costituisce il luogo dei centri delle circonferenze tangenti internamente alle due circonferenza date.
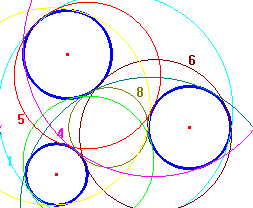
Si capisce a questo punto che le 8 circonferenze cercate avranno i rispettivi centri nell’intersezione di rami dell’iperbole.
Esercizio 11.1:
Costruire un’iperbole assegnati il fuoco e l’asse
Esercizio 11.2:
Costruire la macro che dati un punto e un segmento costruisce l’iperbole avente quel punto come fuoco e quel segmento come asse.
Esercizio 11.3:
Costruire le 8 circonferenze che risolvono il problema di Apollonio