
This is the page
27 Gennaio 2019
è arrivato … il Cantastoria
27 Gennaio 2019di Luigi Pellegrini
1. Costruzione di oggetti: punti, rette, poligoni, curve
Esercizio 1.1:
Costruire un triangolo isoscele che rimanga isoscele anche spostando 1 punto.

Dato il segmento AB, attraverso lo strumento asse costruiamo l’asse r di AB. Creiamo ora un punto C sull’asse r e uniamo C con A e B. Il triangolo ABC si mantiene isoscele anche spostando i punti A, B e C (per spostare un punto utilizzare lo strumento puntatore).
Esercizio 1.2:
Costruire una circonferenza che passi per due punti.

E’ l’esercizio 1.1 considerato da un altro punto di vista. Dati 2 punti A e B, costruire l’asse del segmento AB. Creare un punto O sull’asse e poi, usando lo strumento circonferenza, creare una circonferenza di centro O e raggio OB. Spostando il centro O le circonferenza ottenute passano tutte per A e B.
Esercizio 1.3:
Costruire una circonferenza che passi per tre punti.

Dati i tre punti A, B e C, il punto d’intersezione degli assi dei 2 segmenti AB e BC è il centro della circonferenza cercata. Di nuovo provare a spostare i punti A, B e C: la circonferenza passerà comunque per i 3 punti.
Esercizio 1.4:
Costruire i punti notevoli del triangolo (ortocentro, baricentro, circocentro, incentro).

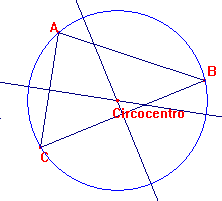
Dato un triangolo ABC, selezionare lo strumento asse e quindi disegnare gli assi di 2 lati AC e CB. Essi si incontrano nel circocentro. Verificare che una circonferenza di centro il circocentro passa effettivamente per A, B e C.
Spostando uno dei tre vertici del triangolo con lo strumento puntatore la circonferenza disegnata passerà comunque per i vertici del triangolo.
Si può fare lo stesso esercizio trovando incentro (punto di incontro delle bisettrici), baricentro (punto di incontro delle mediane) e ortocentro (punto di incontro delle altezze).
